Ch.3 LightGBM完整建模流程的数学推导

  在我们了解了一系列LGBM的数据压缩方法和决策树优化方法之后，本节我们围绕LGBM的损失函数求解过程进行完整的数学推导，同时也将结合此前介绍的LGBM提出的一系列数据预处理方法，从原理层面为大家呈现完整的LGBM算法建模流程。不过正如此前所说，LGBM的损失函数求解过程几乎可以看成是GBDT和XGB的结合体，因此LGBM损失函数的数学推导层面本身并不会有太多难点。但需要注意的是，不同于XGB算法提出了一整套非常严谨的数学推导和逻辑证明，LGBM其实更像是通常意义下的机器学习算法——即一切以后验结果为准。在LGBM算法提出团队来看，很多数学过程并不是一定需要环环相扣，一切以“追求最高精度”为导向，很多数学过程或许可以以“启发式”的方法拼凑到一起，只要最终能够获得一个足够精确的结果和高效的计算过程即可。

  因此，从这个角度来说，学习LGBM算法的难点并不在于数学推导（LGBM算法原理的数学过程不会超过XGB的范畴），但却需要我们将环环相扣的数学过程拆解成一个个独立的关键环节，并理解每个关键环节之于最终结果的影响，同时能够进一步理解不同环节的拼凑组合会有哪些优势和潜在问题，最终建立对GBDT算法框架各算法数学过程更层次理解。

需要注意的是，不仅LGBM是这种启发式的拼接数学过程、一切以后验的结果为准，后续介绍的CatBoost算法也是类似。因此，掌握这种拆分数学过程并进行灵活组装的思维，对于理解新一代GBDT算法至关重要。当然，从另一个角度来说，也能看出XGB算法的数学推导，是目前GBDT类算法无法逾越的理论高峰。

1.LGBM理论推导中的关键数学环节

  这里我们首先回顾GBDT算法和XGB算法在进行原理推导时关键的数学环节，并通过对比两个算法在相同环节的不同数学策略，来分析这些数学策略对最终结果的影响，并探讨LGBM算法在这些关键环节上的选择及其背后的依据。需要注意的是，接下来的内容需要用到大量Lesson 12、Lesson 13中的基础知识，在学习本节内容之前，需要回顾此前课程内容。

  总的来说，GBDT框架算法最核心的数学环节有以下三个，分别是伪残差计算公式、决策树预测结果的计算方法和决策树分裂增益计算方法，此处我们对比GBDT和XGB两个算法在这些不同数学环节采取的不同数学策略，并分析不同数学策略对结果的直接影响：

1.1 关键数学环节一：伪残差计算公式

  • XGB和GBDT伪残差计算公式

  在Lesson 12中我们曾讨论，伪残差并不一定是真正的残差（当评估指标是MSE时，GBDT的伪残差就是残差，不过这只是一个“巧合”），但使用伪残差代替残差，能够非常好的提升模型的收敛效率、提高模型的泛化能力，并且能够大幅提升模型的可用性——即可以灵活定义不同类型的损失函数进行建模，进而拓展模型本身的应用范围。

  并且，在Lesson 12中我们曾证明，伪残差之所以能够加快模型收敛速度，是因为伪残差代表的拟合方向就是损失函数最快速减小（下降）的方向。换而言之，通过一颗颗决策树不断拟合伪残差，最终能够使得损失函数最快速的减小。同时，在伪残差的具体选取上，GBDT的伪残差是样本的负梯度：$$r_{it-GBDT} = -\frac{\partial{l(y_i,H_{t-1}(x_i))}}{\partial{H_{t-1}(x_i)}}$$而XGB的伪残差则是一个同时包含梯度和损失函数二阶导的计算结果：$$g_{ik-XGB} = \frac{\partial{l(y_i,H_{k-1}(x_i))}}{\partial{H_{k-1}(x_i)}}$$

h_{ik-XGB} = \frac{\partial^2{l(y_i,H_{k-1}(x_i))}}{\partial{H^2_{k-1}(x_i)}}$$
$$r_{ik-XGB} = -\frac{g_{ik}}{h_{ik}}$$而根据Lesson 13中的数学推导不难看出，从本质上来说，XGB的伪残差是在拟合损失函数的二阶泰勒展开，而GBDT的伪残差则是在拟合损失函数的一阶泰勒展开。在大多数情况下，通过拟合二阶泰勒展开，能够更好的捕捉损失函数的更加细微的变动，从而提升精度，但代价是这么做需要耗费更大的计算量。 - LGBM伪残差计算公式及选择依据   而对于LGBM来说，却并没有采用看似理论精度更高的XGB伪残差计算策略，而是采用了GBDT的伪残差计算策略。究其原因，其实还是为了加快速度、保证精度。在加快速度方面，正如此前所说，包含二阶导数的伪残差计算过程会耗费更大量的计算资源；而在保证精度方面，则是因为经过实际验证，伪残差的不同选取对最终模型的精度并没有本质上的影响，尽管XGB的伪残差拥有更高的理论精度，但这种精度优势是非常微小的，考虑到实际模型的建模精度还会受到非常多的其他不确定性因素影响，因此XGB的伪残差并不是唯一最好的选择。当然，这里我们可以更进一步的进行讨论，XGB伪残差的理论精度优势之所以很小，是因为对于GBDT类算法来说，伪残差只是迭代的方向，并不是最终迭代的结果，实际拟合效果不仅跟方向有关，更和实际的每颗树的预测结果有关，换而言之，真正能让损失函数数值下降的，其实是决策树输出的预测结果。因此，LGBM判断（同时也是经过实验验证），XGB的伪残差并不能带来非常大的实际建模精度收益，真正对预测结果有显著影响的，是决策树的预测结果以及决策树的生长方式。 #### 1.2 关键数学环节二：决策树的预测结果 - XGB的决策树权重计算公式   对于GBDT来说，决策树的预测结果其实就是简单的叶节点样本均值的计算结果，几乎和普通的CART树的计算过程类似。而XGB则开创性的提出了一种基于样本导数和二阶梯度的预测结果，计算公式如下：$$w_j = -\frac{\sum_{i \in j}g_{i}}{\sum_{i \in j}h_{i} + \lambda}$$其中$w_j$表示第$j$个分支的权重，而$i$则表示这个分支中的第$i$个样本，$h_i$表示第$i$个样本的hessian值，$g_i$表示第$i$个样本的梯度。这里省去了第$k$次迭代的标号。   而根据Lesson 13中的讨论，这种预测结果能够最大程度令损失函数下降。并且在XGB中，叶节点的预测结果被定义成叶节点权重（这么做的原因是因为最终各模型的叠加表达式是一个线性方程，叶节点的输出结果在这个线性方程中就像是一个个变量的权重，用于表示该节点对最终预测结果做出的贡献大小）。 - XGB的决策树权重计算公式只和损失函数有关，和伪残差无关   这里需要重点关注的是，这种设计真正创新之处在于将决策树的叶节点预测结果和损失函数直接挂扣，而非和当前数据集的标签挂钩。尽管从公式层面看起来确实像和XGB的伪残差存在某种关系，但实际上，在Lesson 13的数学推导过程中我们不难发现，这个式子实际上是直接从损失函数的公式中求解得到的，跟伪残差如何计算并没有任何关系。相关证明我们可以从Lesson 13的损失函数公式求解的推导过程中得出，当然，我们也可以用一种更加简单的方式，直接证明上述叶节点的预测结果能够最大程度另损失函数数值下降。   首先，这个问题可以转化为求解损失函数在当前叶节点权重下的最小值，即假设某棵树已经完成生长，叶节点应该如何进行预测，才能令损失函数取得最小值。首先我们简单回顾泰勒展开的表示形式：假设$\delta$是一个非常小的量，则对函数$f(x)$来说，可以将其在 $x$ 点附近的 $f(x+\delta)$ 进行泰勒展开，公式如下： $$f(x+\delta) = f(x) + \delta f'(x) + \frac{1}{2}\delta^2f''(x)+...

其中f′(x)f'(x)是f(x)f(x)的一阶导，f′′(x)f''(x)是f(x)f(x)的二阶导数。

注意，泰勒展开有多种表示，以上只是其中一种表示形式。

当然，具体来看f(x+δ)f(x+\delta)的二阶展开就是 f(x)+δf′(x)+12δ2f′′(x)f(x) + \delta f'(x) + \frac{1}{2}\delta^2f''(x)，因此上述公式也可以写成：

f(x+δ)≈f(x)+δf′(x)+12δ2f′′(x)f(x+\delta) \approx f(x) + \delta f'(x) + \frac{1}{2}\delta^2f''(x)

  类似的，我们假设L(y,f(x))L(y, f(x))是损失函数，其中f(x)f(x)是某次迭代预测结果，并假设下一次预测的结果为δ\delta，那么则有下次迭代之后的损失函数表达式为L(y,f(x)+δ)L(y, f(x)+\delta)，此时我们就L(y,f(x)+δ)L(y, f(x)+\delta)进行二阶泰勒展开，得到公式如下：

L(y,f(x)+δ)≈L(y,f(x))+δL′(y,f(x))+12δ2L′′(y,f(x))L(y, f(x)+\delta) \approx L(y, f(x)) + \delta L'(y, f(x)) + \frac{1}{2}\delta^2 L''(y, f(x))

并且此时L′(y,f(x))L'(y, f(x))就是样本梯度，可以表示为gg，而L′′(y,f(x))L''(y, f(x))则是样本的hessian值，可以表示为hh，同时我们知道，两次迭代之间的δ\delta，其实就是这颗决策树的预测结果乘以学习率的结果，也就是XGB中定义的叶节点权重乘以权重，因此δ\delta也可以用w⋅ηw\cdot \eta进行表示。因此，上述公式等价于：

L(y,f(x)+w⋅η)≈L(y,f(x))+w⋅ηg+12w2⋅η2hL(y, f(x)+w\cdot \eta) \approx L(y, f(x)) + w\cdot \eta g + \frac{1}{2}w^2\cdot \eta^2 h

而我们希望通过这次迭代，能够让损失函数尽可能的减少，即我们希望L(y,f(x)+δ)L(y, f(x)+\delta)尽可能小，也就等价于我们希望表达式L(y,f(x))+wg+12w2hL(y, f(x)) + w g + \frac{1}{2}w^2 h计算得到的结果尽可能小。而其中L(y,f(x))L(y, f(x))是上一次迭代结果，是固定的值，因此最终等价于求解如下表达式：$$min{(w\cdot \eta g + \frac{1}{2}w^2\cdot \eta^2 h)}$$

而在这个表达式中，gg和hh都是已知的结果，因此这个表达式是一个关于ww的函数。而要令其取值最小，我们同样可以对其进行求导，并令导数为0，得到表达式如下：

g⋅η+w⋅η2h=0g\cdot \eta + w\cdot \eta^2 h=0

由此可以得到ww的最佳取值为$$w=-\frac{g}{\eta \cdot h}$$

而η\eta是人工设置的某个常数，因此ww的最佳取值也可以等价为$$w=-\frac{g}{h}$$

对应到第jj个分支，则有如下计算公式：$$w_j = -\frac{\sum_{i \in j}g_{ik}}{\sum_{i \in j}h_{ik} + \lambda}$$

其中λ\lambda是L2正则化项，用于控制模型复杂度。而每个节点的梯度（和hessian）就是对应节点中全部样本求和的结果。

  而通过上面这个过程我们不难发现，XGB的决策树叶节点权重计算公式只和损失函数有关，和伪残差无关。而这样的叶节点预测结果，相比CART树的预测结果（样本标签均值或者多数类类别），毫无疑问能够更好的降低损失函数取值，从而加快迭代效率。

  • LGBM的决策树预测结果计算公式

  也正因如此，LGBM采用了XGB一样的叶节点预测结果计算公式，即$$w_j = -\frac{\sum_{i \in j}g_{ik}}{\sum_{i \in j}h_{ik} + \lambda}$$并且我们知道了这个计算公式的推导实际上只和损失函数有关，而和伪残差无关，因此也解释了为何LGBM和XGB的伪残差不同，但决策树的预测结果计算公式相同的原因。不过需要注意的是，LGBM中并没有叶节点权重这一概念，只是将其称作叶节点预测结果。

1.3 关键数学环节三：决策树分裂增益

  • 决策树分裂增益由叶节点预测结果计算公式直接决定

  需要注意的是，上述决策树预测结果计算公式是基于某棵树已经建立完成后，推导得到的结论。和直观感受相悖的是，对于具体的每棵树如何生长、如何计算分裂增益，其实也是依据叶节点预测结果来进行的推导，即只要给定了叶节点的预测结果计算公式，就能在“最快速降低损失函数取值”这一目标下，推导出分裂增益的计算公式。例如，在XGB中，具体的由叶节点权重推导得到分裂增益的计算公式的过程如下：

  首先，我们将w=−gη⋅hw=-\frac{g}{\eta \cdot h}带入到损失函数L(y,f(x)+w⋅η)L(y, f(x)+w\cdot \eta)表达式中，得到结果如下：

L(y,f(x)+w⋅η)≈L(y,f(x))−gη⋅h⋅ηg+12(−gη⋅h)2⋅η2hL(y, f(x)+w\cdot \eta) \approx L(y, f(x)) -\frac{g}{\eta \cdot h}\cdot \eta g + \frac{1}{2}{(-\frac{g}{\eta \cdot h})}^2\cdot \eta^2 h

计算得到$$L(y, f(x)+w\cdot \eta) \approx L(y, f(x)) -\frac{g^2}{h} + \frac{1}{2}\frac{g^2}{h}=L(y, f(x)) -\frac{1}{2}\frac{g^2}{h}$$

而此时，我们仍然希望损失函数取值足够小，即希望L(y,f(x))L(y, f(x))和12g2h\frac{1}{2}\frac{g^2}{h}足够接近，换而言之，我们希望12g2h\frac{1}{2}\frac{g^2}{h}越大越好。而在XGB中，g2h+λ\frac{g^2}{h+\lambda}也被称作结构分数，其中λ\lambda是L2范数。

注意，这里的12g2h\frac{1}{2}\frac{g^2}{h}是无法超过L(y,f(x))L(y, f(x))的，这个是由函数本身性质决定。

  据此，我们就能得到分裂增益的计算公式了，即希望每次分裂都能够让子节点尽可能的获得一个更大的g2h\frac{g^2}{h}值，即获得一个尽可能大的结构分数。因此XGB分裂增益的计算公式子节点的结构分数减去父节点的结构分数，即为：$$Gain_{XGB} = \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_R + \lambda} - \gamma

其中 $G_L$ 和 $G_R$ 分别表示左子树和右子树的梯度之和，$H_L$ 和 $H_R$ 分别表示左子树和右子树的二阶导数之和，$\lambda$ 是 L2 正则化参数，$\gamma$ 是用于调整树的复杂度的参数。   同时，这里不难看出，分裂增益其实是一种局部最优算法，即希望每次分裂的时候都能够最大程度降低损失函数取值，但局部最优不一定会导致全域最优，因此从更严谨的角度来说，我们其实不能直接说是为了追求损失函数下降最快而设计的分裂增益计算公式。这其实也是XGB算法留给后人有待进一步提高的一个点。 - LGBM的分裂增益计算公式   不过由此，我们也不难发现，分裂增益的计算公式其实是和叶节点的预测结果直接挂钩的，同样也和伪残差的计算公式没有关系。而对于LGBM来说，由于采用了和XGB相同的叶节点预测结果计算公式，因此LGBM的决策树分裂增益计算公式和XGB的类似，基本计算公式如下： $$Gain_{LGBM} = \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_R + \lambda} $$同样的，$G_L$ 和 $G_R$ 分别表示左子树和右子树的梯度之和，$H_L$ 和 $H_R$ 分别表示左子树和右子树的二阶导数之和，$\lambda$表示L2正则化项。而有所不同的是LGBM的分裂增益计算公式中并没有$\gamma$项，并且在LGBM中也并没有结构分数这一概念，只是简单的给出了叶节点预测计算公式和分裂增益计算公式。   而为何LGBM中没有$\gamma$，其实也是因为LGBM的决策树本身生长方式和XGB有很大的不同，正如此前介绍的，LGBM中的决策树是叶节点优先的生长策略（Leaf-wise growth），而XGB中的决策树则是深度优先的生长策略（Level-wise growth），因此LGBM的决策树分裂过程会比XGB的决策树更加敏感，此时如果加入$\gamma$，可能会造成模型本身欠拟合，因此LGBM中并没有引入$\gamma$这一概念。而其他方面，则和XGB的分裂增益计算公式没有任何区别。 - 带有L1正则化项的分裂增益计算公式   上述分裂增益计算公式是官方说明文档和原始论文中推导得到的计算方法，除此之外，我们在Ch.2中还提出了另一种分裂增益计算公式，即$$Gain_{L1} = \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_R + \lambda} - \alpha \cdot (|w_L|+|w_R|)$$这是源码实现过程中分裂增益的计算过程，不难发现，二者区别就在于是否添加了叶节点权重的L1正则化项。而需要注意的是，$Gain_{L1}$和$Gain_{LGBM}$本质上并没有区别，这是当LGBM损失函数中包含L1正则项的时候，将L1正则化在损失函数中发挥作用的方式移植到分裂增益计算过程中的具体体现，是一种近似的计算过程。换而言之，就是将损失函数中的L1正则化的计算过程通过（一定程度的）等价转化关系，放到分裂增益中来进行计算。 - 加入GOSS过程后的分裂增益计算公式   此外，需要注意的是，如果是进行了GOSS抽样，则需要在进行梯度和Hessian值计算时分别计算大梯度样本和小梯度样本的梯度和及Hessian和，然后再令小样本的梯度和及Hessian和乘以膨胀系数、并于大样本对应结果进行相加，得到最终数据集的梯度和及Hessian和。 - LGBM原论文中的分裂增益计算公式   而关于LGBM中决策树的分裂的增益计算公式还有一点需要说明的是，在LightGBM: A Highly Efficient Gradient Boosting Decision Tree (2017)原论文中，简单介绍过LGBM的分裂计算公式，即：

1679823029118 而当GOSS抽样时，分裂增益计算过程如下：
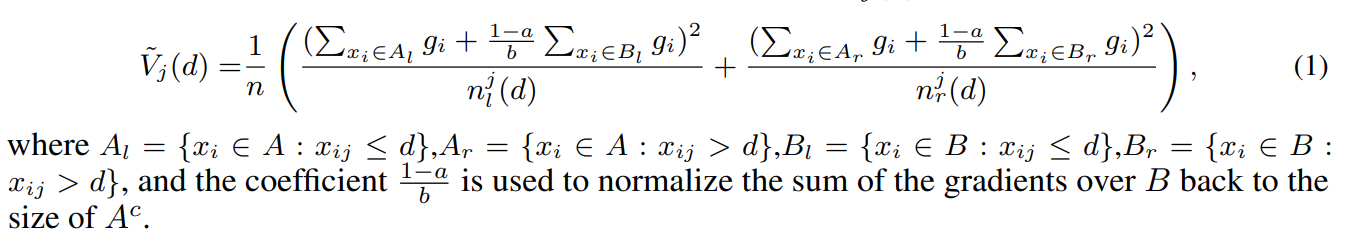1681028026640 其中$n$为父节点的样本总数，$A$和$B$则表示大梯度样本和小梯度样本，$n_l$和$n_r$则表示左子节点、右子节点的样本数，$g_i$表示第$i$条样本的梯度，而$\frac{1-a}{b}$则表示膨胀系数，不难看出，这里的a就是大梯度样本占比，也就是top_rate，而b则是剩余小梯度样本的抽样比例，也就是other_rate。   在这套公式中，并没有明确的“子节点某指标减去父节点某指标”的过程，而只是计算分裂后整体的子节点梯度平方的加权和。并且根据原论文的描述，3.1公式其实就是GBDT的分裂增益计算过程，而下面的公式(1)则是LGBM在进行GOSS抽样时，在GBDT分裂增益计算公式基础上提出的改进策略。但根据官网说明文档的补充说明，这其实只是在某些特定损失函数选取情况下，LGBM的分裂增益才会等价于上述计算公式，更为一般的分裂增益计算公式为此前介绍的$Gain_{LGBM}$计算过程：$$Gain_{LGBM} = \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_R + \lambda}

不得不说，对于LGBM算法学习者来说，很多碎片化的信息和“前后矛盾”的信息，因此想要系统的进行自学的话难度会非常大。而LGBM原论文更是通篇只有三行数学公式（除了上面两个，还有一个是用于计算GOSS过程带来的信息损失），这让我们有理由怀疑，或许这些碎片的信息和“前后矛盾”的信息设计，是出于某种“保密性”需求。相比之下，XGB和CatBoost的论文则“完整”很多。

2.LightGBM完整建模流程的数学推导

  在梳理了LGBM算法原理的核心数学环节之后，让我们结合此前两个小节介绍的LGBM数据处理方法，来进行LGBM的完整建模流程的数学推导。类似的，这里我们同样借助Lesson 13相同的数学符号进行表示。假设现有数据集NN，含有形如(xi,yi)(x_i,y_i)的样本MM个，ii为任意样本的编号，单一样本的损失函数为l(yi,H(xi))l(y_i,H(x_i))，其中H(xi)H(x_i)是ii号样本在集成算法上的预测结果，整个算法的损失函数为L(y,H(x))L(y,H(x))，且总损失等于全部样本的损失之和：L(y,H(x))=∑il(yi,H(xi))L(y,H(x)) = \sum_i l(y_i,H(x_i))。目标函数中使用L2正则化（λ\lambda为0，α\alpha为0）。同时，弱评估器为ff，总共学习KK轮。

2.1 初始化过程

  首先是正是开始训练之前的模型初始化过程，本阶段需要确定损失函数和正是开始迭代之前的初始预测值。和其他GBDT框架算法类似，LGBM同样也支持多种类型的损失函数，甚至可以自定义损失函数，并且，在不同损失函数选择情况下模型初始预测值是不同的。当然，无论是哪种初始值设置，其目的都是为了让损失函数计算结果尽可能的小。即满足如下计算公式：

H0(x)=argminC∑i=1Ml(yi,C)=argminCL(y,C)\begin{aligned} H_0(x) &= \mathop{argmin}_{C} \sum_{i=1}^M l(y_i,C)\\ \\ &= \mathop{argmin}_{C} L(y,C) \end{aligned}

其中yiy_i为真实标签，CC为任意常数。以上式子表示，找出令∑i=1Ml(yi,C)\sum_{i=1}^Ml(y_i,C)最小的常数CC值，并输出最小的∑i=1Ml(yi,C)\sum_{i=1}^Ml(y_i,C)作为H0(x)H_0(x)的值。这里列举几种比较典型的LGBM支持的损失函数，及其初始值计算公式：

  • 均方误差（MSE）：适用于回归问题。初始值是训练数据集目标值的均值，即y_init = np.mean(y_train)；

  • 二分类对数损失（Binary Log Loss）：适用于二分类问题。初始值是训练数据集中正负样本比例的对数几率，即y_init = log(∑(y_train==1) / ∑(y_train==0))；

  • 多分类对数损失（Multiclass Log Loss）：适用于多分类问题。初始值是训练数据集中每个类别的对数几率，即y_init[k] = log(∑(y_train==k) / ∑(y_train!=k))，其中k表示类别；

  • 二分类交叉熵损失（Binary Cross Entropy）：适用于二分类问题。初始值与二分类对数损失相同；

  • Poisson损失：适用于计数回归问题（预测值为非负整且服从泊松分布）。初始值是训练数据集目标值的对数均值，即y_init = log(np.mean(y_train))；

  • Gamma损失：适用于正值回归问题（例如持续的时间或距离计算问题）。初始值是训练数据集目标值的均值除以其方差的对数，即y_init = log(np.mean(y_train) / np.var(y_train))；

  • Tweedie损失：适用非负值回归问题。初始值取决于Tweedie分布的指数参数p。当p接近0时，初始值类似于Poisson损失，当p接近2时，初始值类似于Gamma损失。

2.2 数据压缩过程

  在根据所选择的损失函数得到初始全部数据的预测结果后，接下来就需要来进行数据压缩，也就是Ch.1中介绍的连续变量分箱和EFB降维。分箱的个数和降维的程度，其中，分箱个数可以通过max_bin超参数来进行控制，而降维的程度则可以通过max_conflict_rate超参数来进行控制，并且，max_bin取值越小、max_conflict_rate取值越大，数据压缩就越严重，模型训练速度就更快、模型精度就更低，反之如果max_bin取值越大、max_conflict_rate取值越小，则模型训练速度将有所下降，但模型精度会提高。

  总之这个阶段是围绕全部的样本进行数据压缩，并且会保留压缩过程中的核心信息，如分箱的边界、特征捆绑时的offset，用于处理后续新数据集的特征。

  当完成数据集压缩后，接下来建模的过程只会带入压缩后的数据，原始数据将被舍弃。

2.3 Boosting迭代过程

  接下来进入到Boosting的迭代过程，即单独每颗决策树的训练过程。这里我们假设总共迭代K次，本次迭代过程为第k次，其中k取值范围为[1, k]，本次迭代过程中LGBM将按照如下步骤进行迭代计算：

  • Step 1.GOSS抽样
      在构建每颗树之前，LGBM将按照大小梯度样本划分情况进行GOSS抽样，具体抽样比例受top_rate和other_rate影响，两个超参数取值越大、抽样得到的样本数量越多，反之抽样得到的样本数量就越少。这里我们同样假设第k次迭代时，抽取的数据集为NkN^k，同时计算得到膨胀系数为1−top_rateother_rate\frac{1-top\_rate}{other\_rate}；

  • Step 2.计算伪残差
      在得到了上一轮预测结果Ht−1(x)H_{t-1}(x)和GOSS抽样数据的基础上，我们就可以进行本轮迭代的伪残差计算，伪残差是实际每轮建树时的拟合对象，LGBM的伪残差和GBDT的伪残差完全一样，就是当前样本的负梯度，其中，样本xix_i在这一轮迭代时的伪残差并按照如下公式进行计算：

rki=−∂L(yi,Hk−1(xi))∂Hk−1(xi)r_{ki} = -\frac{\partial L(y_i, H_{k-1}(x_i))}{\partial H_{k-1}(x_i)}

其中L(yi,Hk−1(xi))L(y_i, H_{k-1}(x_i))表示xix_i在本轮计算时的损失函数，而Hk−1(xi)H_{k-1}(x_i)则表示样本xix_i上一轮的预测结果；

  • Step 3.拟合伪残差
      接下来尝试训练一颗决策树来拟合当前样本的伪残差。本阶段LGBM将采用叶节点优先的决策树生长策略，并采用直方图优化加速计算过程。决策树具体生长过程的分裂增益为：$$Gain = \frac{(\sum_{i \in L}g_i)^2}{\sum_{i \in L}h_i + \lambda} + \frac{(\sum_{i \in R}g_i)^2}{\sum_{i \in R}h_i + \lambda} - \frac{(\sum_{i \in P}g_i)^2}{\sum_{i \in P}h_i + \lambda} $$需要注意的是，尽管LGBM拟合的伪残差只有损失函数一阶导，但分裂增益却同时包含损失函数的一、二阶导数。而根本原因在于分裂增益的计算公式由叶节点预测结果决定，而叶节点预测结果则可以由损失函数直接推导得到，跟伪残差没有直接关系。

  • Step 4.输出预测结果
      最后则是输出本轮决策树的预测结果，对任意叶子节点jj来说，输出值为$$w_j = -\frac{\sum_{i \in j}g_{ik}}{\sum_{i \in j}h_{ik} + \lambda}$$假设样本ii被分割到叶子jj上，则有：$$f_k(x_i) = w_j$$对于LGBM来说，叶节点预测结果和XGB完全一致。

  • Step 5.更新损失函数计算结果
      最后，则是根据本轮计算结果，更新损失函数计算结果，即根据预测结果fk(xi)f_k(x_i)迭代模型，具体来说：

H_k(x_i) = H_{k-1}(x_i) + f_k(x_i)$$
假设输入的步长为$\eta$，则$H_k(x)$应该为：

$$H_k(x_i) = H_{k-1}(x_i) + \eta f_k(x_i)$$
对整个算法则有：

$$H_k(x) = H_{k-1}(x) + \eta f_k(x)$$
#### 2.4 Boosting迭代停止   当执行完K轮迭代后，最终输出$H_K(x)$的值作为集成模型的最终预测结果。至此，便完成了模型整体训练过程。   至此，我们就完成了LGBM完整建模流程的数学推导。当然，就像开篇所言，对于LGBM的数学原理方面的学习，重点不在于复杂公式的推导，而在于一些关键数学过程的更深层次理解，LGBM开创性的对不同算法的各关键环节进行“启发式”的组合，并且在一系列数据压缩和抽样方法配合下，达到了高效同时精准的建模水准。当然，至此我们也完成了全部的LGBM基础理论方面的学习，从下一小节开始，我们将进入到LGBM的具体实践环节的学习中，并在实战过程中感受LGBM算法的强大实例。